Ranking SVM
Ranking SVM is an application of Support vector machine, which is used to solve certain ranking problems. The algorithm of ranking SVM was published by Torsten Joachims by 2003.[1] The original purpose of of Ranking SVM is to improve the performance of the internet search engine. However, it was found that Ranking SVM also can be used to solve other problems such as Rank SIFT.[2]
Contents |
Description
Ranking SVM, one of the pair-wise ranking methods, which is used to adaptively sort the web-pages by their relationships (how relevant) to a specific query. A mapping function is required to define such relationship. The mapping function projects each data pair (inquire and clicked web-page) onto a feature space. These features combined with user’s click-through data (which implies page ranks for a specific query) can be considered as the training data for machine learning algorithms.
Generally, Ranking SVM includes three steps in the training period:
- It maps the similarities between queries and the clicked pages onto certain feature space.
- It calculates the distances between any two of the vectors obtained in step 1.
- It forms optimization problem which is similar to SVM classification and solve such problem with the regular SVM solver.
Background
Ranking Method
Suppose  is a data set containing
is a data set containing  elements
elements 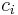 .
.  is a ranking method applied to
is a ranking method applied to  . Then the
. Then the  in
in  can be represented as a
can be represented as a  by
by  asymmetric binary matrix. If the the rank of
asymmetric binary matrix. If the the rank of 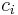 is higher than the rank of
is higher than the rank of 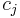 , i.e.
, i.e. 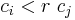 , the corresponding position of this matrix is set to value of "1". Otherwise the element in that position will be set as the value "0".
, the corresponding position of this matrix is set to value of "1". Otherwise the element in that position will be set as the value "0".
Kendall’s Tau [3][4]
Kendall's Tau also refers to Kendall tau rank correlation coefficient, which is commonly used to compare two ranking methods for the same data set.
Suppose 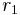 and
and 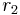 are two ranking method applied to data set
are two ranking method applied to data set  , the Kendall's Tau between
, the Kendall's Tau between 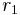 and
and 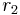 can be represented as follows:
can be represented as follows:
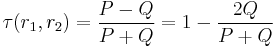
where  is the number of the same elements in the upper triangular parts of matrices of
is the number of the same elements in the upper triangular parts of matrices of 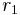 and
and 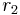 ,
,  is the number of the different elements in the upper triangular parts of matrices of
is the number of the different elements in the upper triangular parts of matrices of 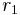 and
and 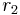 . The diagonals of the matrices are not included in the upper triangular part stated above.
. The diagonals of the matrices are not included in the upper triangular part stated above.
Information Retrieval Quality [5][6][7]
Information retrieval quality is usually evaluated by the following three measurements:
- Precision
- Recall
- Average Precision
For an specific query to a database, let 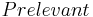 be the set of relevant information elements in the database and
be the set of relevant information elements in the database and 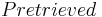 be the set of the retrieved information elements. Then the above three measurements can be represented as follows:
be the set of the retrieved information elements. Then the above three measurements can be represented as follows:

where 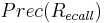 is the Precision function of
is the Precision function of 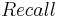 .
.
Let 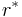 and
and 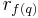 be the expected and proposed ranking methods of a database respectively, the lower bound of Average Precision of method
be the expected and proposed ranking methods of a database respectively, the lower bound of Average Precision of method 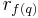 can be represented as follows:
can be represented as follows:
![AvgPrec(r_{f(q)}) \geqq {1 \over R} \left[ Q%2B \binom{R%2B1}{2} \right ]^{-1}(\sum_{i=1}^R\sqrt{i})^2](/2012-wikipedia_en_all_nopic_01_2012/I/ca688821c71077c791d937eed4e22ebd.png)
where  is the number of different elements in the upper triangular parts of matrices of
is the number of different elements in the upper triangular parts of matrices of 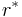 and
and 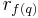 and
and  is the number of relevant elements in the data set.
is the number of relevant elements in the data set.
SVM Classifier [8]
Suppose 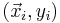 is the element of a training data set , where
is the element of a training data set , where 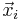 is the feature vector (with information about features) and
is the feature vector (with information about features) and 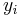 is the label(which classifies the category of
is the label(which classifies the category of 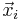 ). An typical SVM classifier for such data set can be defined as the solution of the following optimization problem.
). An typical SVM classifier for such data set can be defined as the solution of the following optimization problem.
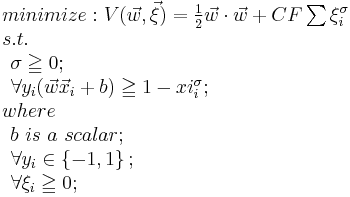
The solution of the above optimization problem can be represented as a linear combination of the feature vectors  s.
s.
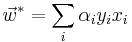
where 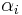 is the coefficients to be determined.
is the coefficients to be determined.
Ranking SVM algorithm
Loss Function
Let 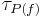 be the Kendall's tau between expected ranking method
be the Kendall's tau between expected ranking method 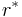 and proposed method
and proposed method 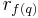 , it can be proved that maximizing
, it can be proved that maximizing 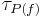 helps to minimize the lower bound of the Average Precision of
helps to minimize the lower bound of the Average Precision of 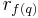 .
.
- Expected Loss Function [9]
The negative 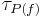 can be selected as the loss function to minimize the lower bound of Average Precision of
can be selected as the loss function to minimize the lower bound of Average Precision of 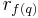
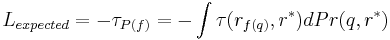
where 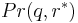 is the statistical distribution of
is the statistical distribution of 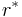 to certain query
to certain query  .
.
- Empirical Loss Function
Since the expected loss function is not applicable, the following empirical loss function is selected for the training data in practice.
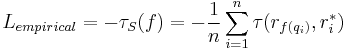
Collecting training data
 i.i.d. queries are applied to a database and each query corresponds to a ranking method. So The training data set has
i.i.d. queries are applied to a database and each query corresponds to a ranking method. So The training data set has  elements. Each elements containing a query and the corresponding ranking method.
elements. Each elements containing a query and the corresponding ranking method.
Feature Space
A mapping function 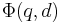 [10][11] is required to map each query and the element of database to a feature space. Then each point in the feature space is labelled with certain rank by ranking method.
[10][11] is required to map each query and the element of database to a feature space. Then each point in the feature space is labelled with certain rank by ranking method.
Optimization problem
The points generated by the training data are in the feature space, which also carry the rank information (the labels). These labeled points can be used to find the boundary (classifier) that specifies the order of them. In the linear case, such boundary (classifier) is a vector.
Suppose 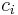 and
and 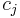 are two elements in the database and denote
are two elements in the database and denote 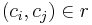 if the rank of
if the rank of 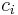 is higher than
is higher than 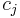 in certain ranking method
in certain ranking method  . Let vector
. Let vector 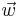 be the linear classifier candidate in the feature space. Then the ranking problem can be translated to the following SVM classification problem.Note that one ranking method corresponds to one query.
be the linear classifier candidate in the feature space. Then the ranking problem can be translated to the following SVM classification problem.Note that one ranking method corresponds to one query.
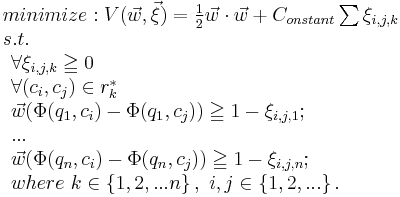
The above optimization problem is identical to the classical SVM classification problem, which is the reason why this algorithm is called Ranking-SVM.
Retrieval Function
The optimal vector 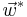 obtained by the training sample is
obtained by the training sample is
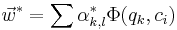
So the retrieval function could be formed based on such optimal classifier.
For new query  , the retrieval function first projects all elements of the database to the feature space. Then it orders these feature points by the values of their inner products with the optimal vector. And the rank of each feature point is the rank of the corresponding element of database for the query
, the retrieval function first projects all elements of the database to the feature space. Then it orders these feature points by the values of their inner products with the optimal vector. And the rank of each feature point is the rank of the corresponding element of database for the query  .
.
Ranking SVM application
Ranking SVM can be applied to rank the pages according to the query. Click-through data is needed to train the algorithm, where Click-through data includes three parts:
- Query.
- Page rank obtained by previous trained result.
- Pages that user clicks.
The combination of 2 and 3 cannot provide full training data order which is needed to apply full svm algorithm. Instead, it provides a part of the ranking information of the training data. So the algorithm can be slightly revised as follows.
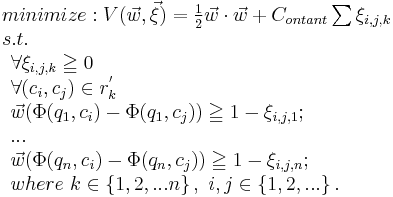
The method 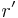 does not provide ranking information of the whole dataset, it's a subset of the full ranking method. So the condition of optimization problem becomes more relax compared with the original Ranking-SVM.
does not provide ranking information of the whole dataset, it's a subset of the full ranking method. So the condition of optimization problem becomes more relax compared with the original Ranking-SVM.
Reference
- ^ Joachims, T. (2003), "Optimizing Search Engines using Clickthrough Data", Proceedings of the ACM Conference on Knowledge Discovery and Data Mining
- ^ Bing Li; Rong Xiao; Zhiwei Li; Rui Cai; Bao-Liang Lu; Lei Zhang; "Rank-SIFT: Learning to rank repeatable local interest points",Computer Vision and Pattern Recognition (CVPR), 2011
- ^ M.Kemeny . Rank Correlation Methods, Hafner, 1955
- ^ A.Mood, F. Graybill, and D. Boes. Introduction to the Theory of Statistics. McGraw-Hill, 3edtion,1974
- ^ J. Kemeny and L. Snell. Mathematical Models in THE Social Sciences. Ginn & Co. 1962
- ^ Y. Yao. Measuring retrieval effectiveness based on user preference of documents. Journal of the American Society for Information Science, 46(2): 133-145, 1995.
- ^ R.Baeza- Yates and B. Ribeiro-Neto. Modern Information Retrieval. Addison- Wesley-Longman, Harlow, UK, May 1999
- ^ C. Cortes and V.N Vapnik. Support-vector networks. Machine Learning Journal, 20: 273-297,1995
- ^ V.Vapnik. Statistical Learning Theory. WILEY, Chichester,GB,1998
- ^ N.Fuhr. Optimum polynomial retrieval functions based on the probability ranking principle. ACM TRANSACTIONS on Information Systems, 7(3): 183-204
- ^ N.Fuhr, S.Hartmann, G.Lustig, M.Schwantner, K.Tzeras,and G.Knorz. Air/x - a rule-based multistage indexing system for large subject fields. In RIAO,1991